Servicios Personalizados
Articulo
Indicadores
Links relacionados
 Citado por SciELO
Citado por SciELO
 Similares en SciELO
Similares en SciELO
Bookmark
Revista Varianza
versión impresa ISSN 9876-6789
Revista Varianza n.17 La Paz nov. 2020
ARTÍCULOS DE INVESTIGACIÓN
Números de Bernoulli y aplicaciones del cálculo
complejo a la estadística
Lic. Raúl León Delgado Álvarez
![]() dea_5@hotmail.com
dea_5@hotmail.com
Resumen
Los trabajos de notables Matemáticos y Estadísticos, como Bernoulli, Cauchy, Hadamard hacen ver que las aplicaciones en el campo de la Estadística son de mucha utilidad y su tratamiento a través del Cálculo Complejo tiene ventajas comparativas que ayudan a la comprensión de sus aplicaciones.
Palabras clave: Función Analítica, números de Bernoulli, series de Laurent
Abstract
The works of notable Mathematicians and Statisticians, such as Bernoulli, Cauchy, Hadamard show that the applications in the field of Statistics are very useful and their treatment through Complex Calculus has comparative advantages that help to understand their applications.
Keywords: Analytical function, Bernoulli numbers, Laurent series
1. INTRODUCCIÓN
Son muchas las aplicaciones al campo de la teoría Estadística las que aporta el Cálculo complejo, aquellas en las que no es suficiente el campo de los números reales, como recurso para justificar las características de la las funciones de probabilidad y el soporte contable de las mismas, es por ejemplo importante justificar la convergencia de una suma infinita como:
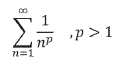
que para p = 2 converge hacia el valor π2/6, o equivalentes para hallar características numéricas de las funciones de probabilidad o demostrar éstas que no existen.
El presente artículo mostrará una aplicación del Cálculo Complejo para problemas similares al considerar expansiones dentro de ese campo.
2. DESARROLLO
Sean dos series de potencias:
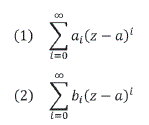
donde r y g son los radios de convergencia de las series (1) y (2) de coeficientes, números positivos, además b0≠ 0.
Si σ = min (r y g), si r = g = α
Entonces ambas series serán convergentes en el círculo ![]() , si en este círculo hay ceros de la expansión:
, si en este círculo hay ceros de la expansión:
![]()
Se toma un nuevo circulo de radio menor en cuyo interior, la suma (2) no se anule, existe puesto que el punto a no es cero de la suma (2) debido a la condición de que b0≠ 0 así entonces existe un circulo ![]()
En el cual ambas series (1) y (2) son convergentes y la suma de la serie (2) carece de ceros.
En el interior de este círculo la relación
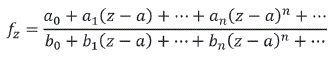
Representa una función analítica la cual consecuencia de la regla de derivación del cociente; por lo tanto, existe una serie de potencias ![]()
Que expresa a la función f(z) en el entero del círculo ![]() cociente de las series (1) dividendo y (2) divisor, realizando la división por el método de los coeficientes indeterminados (algoritmo de la división)
cociente de las series (1) dividendo y (2) divisor, realizando la división por el método de los coeficientes indeterminados (algoritmo de la división)
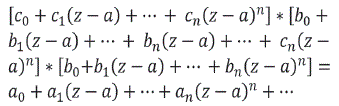
Obsérvese que siendo convergente en el interior del círculo |z - a|< R tiene que ser absolutamente convergente, por eso pueden multiplicar miembro a miembro
Realizando la multiplicación se obtiene:
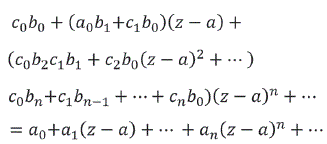
Como las sumas de las series de potencias que figuran en el primer y segundo miembro coinciden en el circulo ![]() según el teorema de identidad para los series de potencias los coeficientes de ambos series tienen que ser iguales, de donde de resultan los ecuaciones
según el teorema de identidad para los series de potencias los coeficientes de ambos series tienen que ser iguales, de donde de resultan los ecuaciones
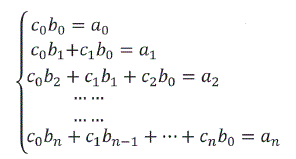
Es un sistema infinito de ecuaciones lineales respecto de los coeficientes desconocidos c0,c1,c2...,cn la particularidad de este sistema simplifica su solución y consiste en que para cualquier n, (n=0,1,2,3,....), las primeras (n+1) ecuaciones contienen las (n+1) incógnitas de las primera ecuación c0 = a0 / b0 , (b ≠ 0 según la hipotesis) y sustituyen dos en la segundo se obtiene
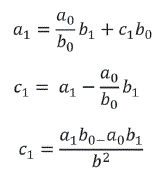
Sustituyendo que en la segunda se han hallado las líneas c0 c1 ... cn-1 , sustituyendo en la (n+1) ecuación se obtiene
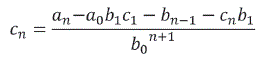
Así se puede encontrar el coeficiente de un índice previamente dado, decir cn en función de a0 ,a1 ,..., an, b0,b1 ,...,bn en forma de la determinada
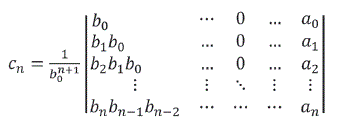
Ejemplo ![]() esta función analítica en todos los puntos del plano a excepción de los ceros de ez-1 es decir a excepción de los puntos
esta función analítica en todos los puntos del plano a excepción de los ceros de ez-1 es decir a excepción de los puntos ![]()
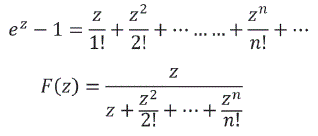
Dividiendo F(z) entre z
![]()
Incluso vale por z = 0
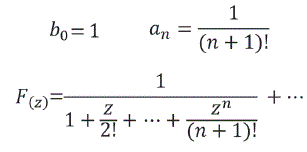
La serie del denominador es convergente para cualquier z y tiene los mismos ceros que la función ez-1, a excepción de un cero en el origen de coordenadas por tanto en el interior del círculo ![]() la suma no se anula la primera de las ecuaciones da:
la suma no se anula la primera de las ecuaciones da:
![]()
Como todos los coeficientes de la serie del dividendo a excepción del coeficiente inicial, son iguales a cero, la (n+1) ecuación tiene la forma:
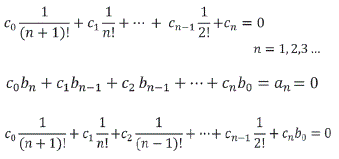
También se puede utilizar la formula por el determinante, es decir
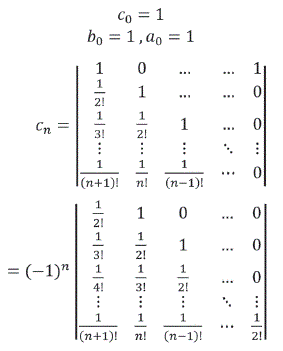
Los números cn n! se denominan números de Bernoulli y designan mediante Bn ; Bn = Cn! Así

De donde se obtiene:
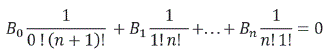
Multiplicando ambos lados de la igualdad por (n+1)! y observando que ![]() es el coeficiente binomial
es el coeficiente binomial ![]() se tiene
se tiene
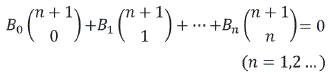
Esta fórmula puede representarse en la siguiente forma
![]()
Como B0 = 1
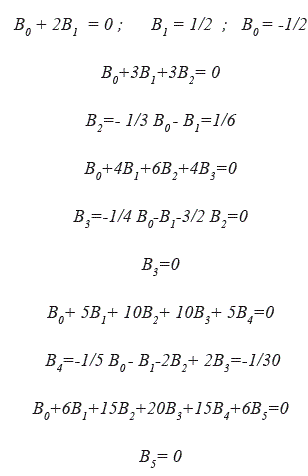
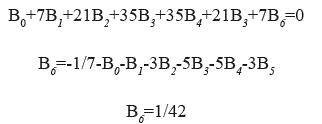
Es decir
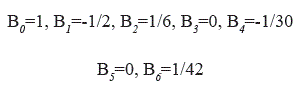
Se demuestra que todos los números de Bernoulli de subíndices impares mayores que la unidad son iguales que B2k+1= 0, k = 1,2,3...
En ![]() sustituyendo z por (-z) en el desarrollo
sustituyendo z por (-z) en el desarrollo
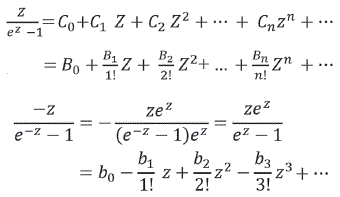
Sumando
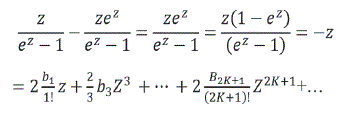
Basándose en la unicidad del desarrollo de la serie de -z y la última expresión se tiene
![]()
Solo B1 = -1/2 los demas B2k+1= 0 para todo k=1,2...
De esta manera el cociente solicitado se puede escribir como:
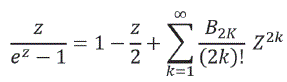
Como los puntos singulares de la función ![]() más próximos al origen de coordenadas son Z1 = 2πi, Z2=-2πi
más próximos al origen de coordenadas son Z1 = 2πi, Z2=-2πi
En estos puntos la función no está definida y no puede definirse de modo que se conserve la continuidad el radio de convergencia de la serie es 2π.
De esta relación según la fórmula de Cauchy-Hadamard se define que
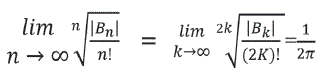
B2K+1= 0, k=1,2,3, por lo tanto, para cualquier ∈ > 0 , existe un conjunto infinito de números B2k que satisfacen la desigualdad
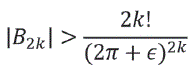
Es decir son muy grandes en comparación con sus índices 2k.
Del desarrollo anterior se pueden obtener los desarrollos de las funciones de zcotgz; tagz; zcosec z al hacer
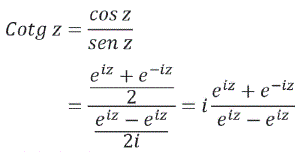
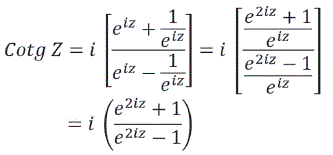
Se puede revisar como
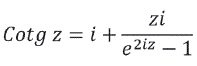
De donde
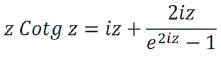
La función: ![]() se puede desarrollar de acuerdo a
se puede desarrollar de acuerdo a
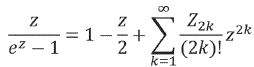
Haciendo 2iz como variable nueva que converge para ![]() , el cociente:
, el cociente:
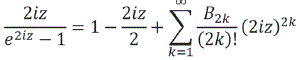
lo que significa:
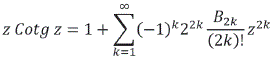
Considerando identidades trigonométricas se puede expresar como
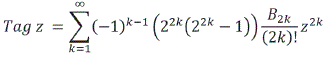
Donde ![]() , también para la
, también para la
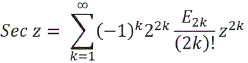
Donde ![]() , los coeficientes E2k se denominan números de Euler, y se determinan por las ecuaciones:
, los coeficientes E2k se denominan números de Euler, y se determinan por las ecuaciones:
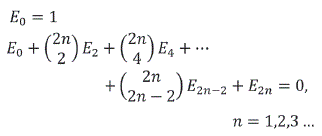
Algunos términos serán:
![]()
Del desarrollo en serie de Laurent para un punto arbitrario z ∈ D
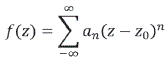
donde los coeficientes
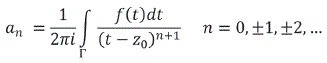
donde ![]()
Donde ![]() los coeficientes an son complejos, pero los λn son números reales no negativos que satisfacen:
los coeficientes an son complejos, pero los λn son números reales no negativos que satisfacen:
λn+1› λn![]()
Dicha serie se denomina serie de Dirichlet general y los lambda se llaman exponentes de la serie, de esta manera ![]() se conoce como la serie de Dirichlet ordinaria o clásica.
se conoce como la serie de Dirichlet ordinaria o clásica.
Escribiendo el desarrollo en serie de Laurent
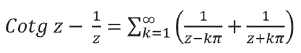
integrando término a término a lo largo de la curva arbitraria que pasa por origen de coordenadas y no pasa por kπ k=1, 2, 3.....
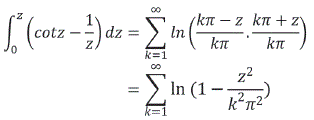
Interpretando la suma infinita como un límite de una suma, se tiene:
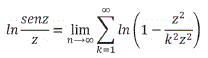
Donde ![]()
pero:
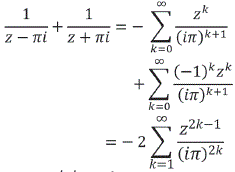
para |z| < πi
Por lo tanto los coeficientes de las potencias pares de z, en el desarrollo de cotg z -1/z son iguales a cero, mientras que los impares se expresan como:
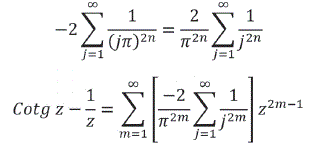
También se mostró el desarrollo:
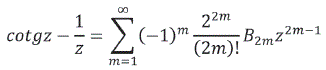
Comparando los dos desarrollos se tiene:
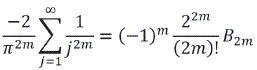
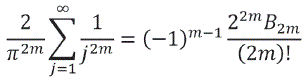
De donde despejando:
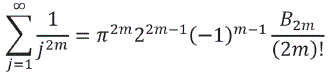
Finalmente para distintos valores de m se tienen las sumas siguientes
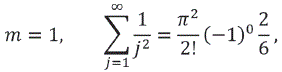
porque B2 = 1/6 , realizando operaciones:

pero B4=(-1)/30, realizando operaciones
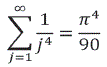
m=3, considerando B6=1/42
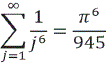
De esta manera se pueden obtener varias sumas.
3. CONCLUSIONES
En el desarrollo del presente artículo, se pudo observar que el tratamiento desde el punto de vista del Calculo Complejo, primero observando las ventajas de operaciones básicas como la división entre polinomios dentro del campo complejo, permite analizar las ventajas de trabajar con funciones analíticas, posteriormente haciendo uso del desarrollo de serie de Laurent, se pueden comparar desarrollos de series que al igualar coeficientes da lugar a sumas infinitas como las que se pudo observar al final del desarrollo.
Aunque esta manera de obtener sumas infinitas no es la única, dado que se pueden comparar con desarrollos de Fourier para obtener los anteriores resultados.
Cuando se hace uso de las fórmulas de Euler Mac Laurin, las mismas son muy laboriosas el método expuesto aquí puede simplificar muchos cálculos innecesarios dado que se puede considerar los números de Bernoulli como elementos ya desarrollados y así obtener más fácilmente las indicadas sumas infinitas.
BIBLIOGRAFÍA
1. Alexei Ivanovich MARKUSHEVICH, Teoría de las funciones de variable Compleja, Editorial MIR. Moscú. [ Links ]
2. Jerrold E. MARSDEN, Michael HOFFMAN, Análisis Básico de Variable Compleja, Editorial Trillas. [ Links ]
3. KRASNOV M.L.KISELIOV, A, I MAKARENKO, Funciones de Variable Compleja Editorial MIR Moscú. [ Links ]












